A figura ao lado mostra um hexágono regular ABCDEF e os pontos médios P, Q, R, S e T dos lados AB, CD, DE, EF e FA, respectivamente.

OBMEP 2021 - QUESTÃO 05 A figura ao lado mostra um hexágono regular ABCDEF e os pontos médios P, Q, R, S e T dos lados AB, CD, DE, EF e FA, ...

OBMEP 2021 - QUESTÃO 05

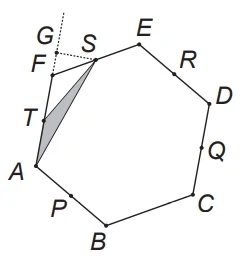
A figura ao lado mostra um hexágono regular ABCDEF e os pontos médios P, Q, R, S e T dos lados AB, CD, DE, EF e FA, respectivamente.

a) Se a área do triângulo AST for igual a 1 cm², qual será a área do triângulo FTS?

b) Qual é a razão entre as áreas dos triângulos APR e PBQ?

c) Qual é a razão entre as áreas sombreada e não sombreada na figura abaixo?

QUESTÃO ANTERIOR:

- Julieta calcula as somas do tipo  da seguinte maneira: ela pensa no número  multiplica-o por 10 e subtrai n. 

RESOLUÇÃO:

Item A

Os triângulos AST e FTS têm a mesma área e, portanto, a área de FTS é igual a 1 cm². De fato, o segmento GS, na figura, é perpendicular à reta que contém os lados AT e TF dos triângulos AST e FTS e é a altura comum desses triângulos relativa a esses lados. Como T é ponto médio de AT, os triângulos AST e FTS têm a mesma área.

Item B

A razão entre as áreas dos triângulos APR e PBQ é 

De fato, os lados AP e PB dos triângulos APR e PBQ, respectivamente, são colineares e têm a mesma medida. Os segmentos paralelos a eles, pelos pontos médios T, S e pelo vértice F do hexágono, como indicado na figura ao lado, dividem as alturas dos triângulos APR e PBQ na razão  pois esses segmentos paralelos a AB e ED, recém-traçados são equidistantes.

Como as bases têm a mesma medida, a razão entre as áreas coincide com a razão entre as alturas e é igual a 

Item C

Para calcular a razão entre as áreas sombreada e não sombreada, façamos o seguinte: tracemos os segmentos AEe P’R’, paralelos à diagonal BD do hexágono ABCDEF, sendo P’ e R’ determinados pela intersecção da reta paralela a BD passando pelo vértice F com os prolongamentos dos lados BA e DE, respectivamente, conforme a figura à esquerda.

Esses segmentos determinam um paralelogramo BDR’P’, que é um retângulo (os ângulos ABD e BDE são retos).

Além disso, como o triângulo BCD tem a mesma área que a reunião dos triângulos AFP´ e ER´F, por congruência, o retângulo BDR’P’ tem a mesma área que o hexágono original, que denotaremos por H.

Podemos comparar a área de cada um dos triângulos sombreados com a área H do hexágono.

• A área do triângulo APR é a metade da área do retângulo APRE, que, por sua vez, é igual a 

Daí, a área desse triângulo é igual a 

• A área do triângulo PBQ é  da área do triângulo APR, conforme visto no item b) e, portanto, sua área será 

• A área do triângulo AST é metade da área do triângulo ASF — vide item a) —, que, por sua  vez, é igual a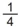 da área do retângulo P´AER´, portanto, sua área será 

Temos, portanto, que a área sombreada é  e, consequentemente, a área não sombreada é igual a 

Conclusão: a razão entre as áreas sombreada e não sombreada é igual a 

PRÓXIMA QUESTÃO:

- Cinco pedras, A, B, C, D e E, estão dispostas como na figura. Kiko, o sapo simpático, pula de uma pedra para outra somente se elas estiverem ligadas por um segmento. Assim, ele pode pular, partindo de A, para B ou D, mas não para E ou C. Por exemplo, começando em A e terminando em D, ele pode realizar o seguinte passeio de 5 pulos: A → B → E → D → C → D.

QUESTÃO DISPONÍVEL EM:

- Provas OBMEP 2021 com Gabarito e Resolução